Логистическое отображение, часто связываемое с именем Фейгенбаума, задается простой формулой:
Значение xn+1 однозначным образом определяется значением предшествующего члена последовательности, xn. Чем-то это похоже на разговор — разговор, в котором каждая следующая реплика вполне логичным образом вытекает из предыдущей. Аналогию можно было бы расширить — сказать, скажем, что xn – развитие темы, (1 – xn) — возражения, а r — усредненная длина ассоциативных цепочек, но, пожалуй, всё же не стоит. Общность не столь велика, чтобы искать прямые соответствия.
Что происходит, когда мы задаемся произвольным начальным значением x0 таким, что 0<x0<1, и начинаем вычислять значения членов последовательности? Начинаем диалог с какой-то темы и говорим, говорим долго, устремляя n к бесконечности?
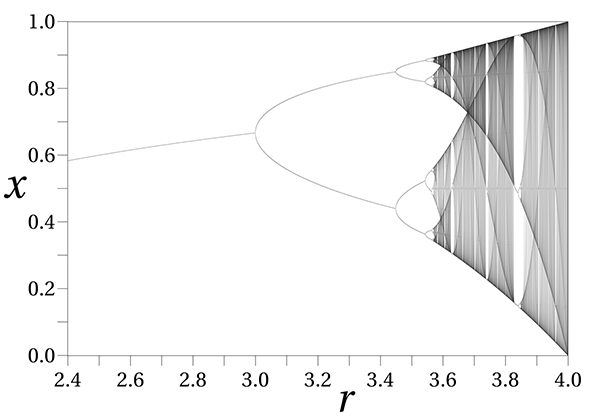
Бифуркационная диаграмма. По вертикальной оси отложены значения, принимаемые членами последовательности Xn+1 = rxn(1-xn) при заданном r при n→∞.
При 1<r<3 последовательность сходится к значению (r-1)/r. Вероятно, каждому доводилось иметь дело с сообществами, в которых любая начатая дискуссия неизменно приходит к одному и тому же выводу.
1<r<1+60,5. Последовательность быстро начинает осциллировать между двумя значениями. Так многие мечутся годами между двумя противоречивыми категоричными утверждениями.
Потом наблюдаются осцилляции между четыремя значениями. Восемью. Шестнадцатью...
Самое же интересное начинается, когда r переваливает за ~3,57. Система приходит в состояние динамического хаоса, периодичность утрачивается. Без выполнения всех необходимых вычислений значение xn становится невозможно предсказать даже приблизительно. Малейшее, незаметное искажение начальных данных — на тысячную, на миллионную долю — непредсказуемым образом радикально изменяет поведение последовательности при больших n. Так из случайной фразы рождаются произведения искусства, революционные теории и жизненные пути.
Вывод, который, собственно, хотелось бы сделать, прост – непредсказуемость не равна нелогичности, и рациональность не есть предначертанность. Отображение Фейгенбаума переходит в хаотический режим, оставаясь всё той же простейшей алгебраической формулой, не использующей никаких генераторов случайных чисел или чего-то в таком духе. А значит, очень вероятно, что все шансы добиться схожего результата есть и у диалога. Внутреннего ли, внешнего — не так важно.
А те, кто уверенно заявляет, что аналитический подход губителен для полета фантазии, просто никогда не видели, как последовательность Xn+1 = rxn(1-xn) ведет себя, скажем, при r=3,87.