До границ применимости аналогии and beyond, знание/опыт и проблема просачивания (percolation).
Задача о просачивании ставится на N-мерной решетке, каждый узел которой соединен с k соседними (2 и 4 в случае простейшей двумерной сетки «тетрадка в клеточку», 3 и 6 – для массива трехмерных кубиков). Каждый узел с вероятностью P может оказаться «открытым», образующим связи с соседними узлами, и с вероятностью 1-P – «закрытым». Теория просачивания изучает свойства кластеров, состоящих из связанных узлов. Простейшая физическая интерпретация, от которой и происходит название – собственно, просачивание жидкости через пористую среду. От наличия достаточно большого кластера, соединяющего стенки рассматриваемого объема, зависит, будет ли он проницаемым или герметичным.
Той же моделью описывается «колонизация» решетки, начинающаяся с одного из узлов. Расширение «обитаемого кластера» продолжается, пока на его границе есть открытые узлы. В качестве узлов могут выступать, скажем, звезды Галактики, если предположить, что перелеты возможны лишь между ближайшими соседними; такой подход применяется в статье «The Fermi Paradox: An Approach Based on Percolation Theory» (Geoffrey A. Landis. 1998. Journal of the British Interplanetary Society, 51, 163-166), из которой взята картинка для привлечения внимания. Можно рискнуть и предположить, что узлами могут быть единицы знания.
(Предполагать, что потенциально доступное человеку знание упорядочено настолько, что связи между его областями могут быть представлены в виде многомерной решетки, конечно, изрядная наглость, но история философии, научпопа и сектантства видела еще и не такое).
Итак, человек колонизирует знание, начиная с некоего затравочного кластера; относительно каждой его порции он принимает решение «любопытно» (и продолжает изучать соседние области) или «тут всё ясно» (и прекращает исследование в данном направлении).
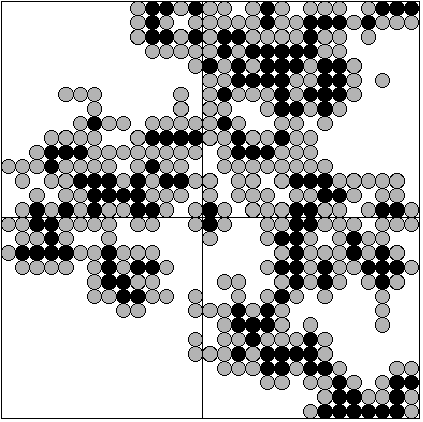
Ради чего все? Ради красивой картинки, возникающей в нетривиальном случае. Тривиальных случаев два: если вероятность P слишком мала, колонизация быстро останавливается, освоенный фрагмент знания оказывается полностью окруженным областями, про которые всё ясно (тут надо обязательно желчно сказать «и все мы видели таких людей»). Если вероятность P велика, колонизация охватывает всё доступное пространство, оставляя лишь небольшие случайные «пузырьки» неосвоенных областей, и продолжается, пока есть время (буйные оптимисты таких людей видели, остальные в их существовании сильно сомневаются). И есть промежуточные значения P, близкие к некоторому критическому (зависящему от N и k); картинка для привлечения внимания (один из двумерных срезов трехмерной решетки, чёрные узлы — открытые, серые — граничные закрытые) сгенерирована как раз для такого варианта.
При околокритическом значении P колонизированная область – доступное человеку знание – приобретает фрактальные черты.
У неё сложной, непредсказуемой формы границы. И в ней есть как сколь угодно большие заполненные, так и сколь угодно большие пустые области.
Натяжками и допущениями картинка для привлечения внимания превращается в иллюстрацию к расхожему, в общем-то, тезису: сколь угодно большое количество знаний не гарантирует их наличия в конкретной удалённой точке, сколь угодно большое количество пробелов в них – не гарантирует отсутствия. Приятного просачивания.
• норкоман штоле #прастити • ai212983
• Спасибо. Посмотреть на это с точи зрения percolation theory новая мысль. Я представляю это как матрицу объектов с наложенным графом. Связность одного участка абсолютно не гарантирует наличия связности с другим. Каждый объект - узел с неизвестным количеством связей, сам является подграфом с фрактальной структурой. Каждая связь в общем случае тоже подграф. Вырожденный крайний случай графа это битфлип, но на таком уровне не имеет осмысленного представления в виде знания (кроме редких случаев когда знание кодируется битом). Остаётся открытым вопрос где проходит граница между информацией в общем и тем что мы можем назвать "знанием". У меня есть смутный ответ на этот вопрос, но смоделировать его формально слишком сложно. вкратце, я считаю что ответ на этот вопрос кроется в кодировании локального состояния "наблюдателя", опять в крайнем случае наблюдатель это физ. система с стойчивым локальным состоянием которое сохраняется в ответ на смену инпута, но в деталях вся эта хуйня сложновата для описания. Это описание в принципе эквивалентно в одном из своих аспектов тому что ты написал выше, но percolation theory явно даёт похожие выводы на более удобной для анализа модели. Я правда предпочитаю сетевые модели вероятностным но они гораздо хуже анализируются, это правда мой bias связаный с бэкграундом, я все таки совсем не знаю физики. • ayoshi
• ^ «Татарский пошевелил в воздухе пальцами, подбирая слова. — На уровне коллективного бессознательного» © / О, я когда-то даже придумал слова mindent — «форма жизни» в информационном пространстве, способная к размножению, мутациям, гибридизации и образованию симбиотических связей; некие «чёрные ящики», исчерпывающее предсказание реакции которых на произвольное внешнее воздействие является задачей низкой вычислительной сложности; могут быть разбиты на минденты более низкого порядка и могут образовывать миндент более высокого порядка) — и mindoplex, у которого количество связей переходит в новое качество и предсказуемость теряется (as in теория хаоса). (В отдельных случаях миндент может локализоваться в одном особенно нажористом Chief Executive Neuron, но вообще это абстракция уровнем-двумя выше, чем просто описание состояния нейросетки). И в рамках этой модели «наблюдатель» как личность — сильносвязанное миндоплекс-ядро, отвлеченные знания в духе «Лондон — столица Парижа» — слабосвязанные минденты на условной периферии, какой-то качественной резкой границы между ними нет. Т.е., близко к твоему описанию — наблюдатель и знание есть некие локально (во времени) устойчивые системы логических вентилей, обрабатывающие входную «информацию в общем». • aldragon
• (Потом я посмотрел на агитационные картинки «философ до придумывания новых слов / через два года после», понял, что с терминогенезом не шутят, и завязал! Почти). • aldragon
• ^^ да, про качественные границы согласен, я когда то писал что они нечеткие, точно так же как провести границу между ent / plex не представляется возможным. Прикольно, что статистически распределить объекты на классы ent/plex относительно просто, очень очень малая часть их будет лежать в области перехода, это в принципе состояние неустойчивого равновесия. • ayoshi
• ^^ ещё отвлеченная мысль, кмк словотворчество должно нас ебать только во время публикации, я например все эти модели даже не формализую, они меня интересуют исключительно как источник выводов, проходная порода. У них есть поганое свойство форматировать мозг: махнёшь хвостом уверенно, глядишь ты уже автор двенадцатитомника про торсионные поля за которым теперь нужно окапываться с целью круговой обороны. С возрастом отваливается все, то что осталось возможно и будет иметь смысл зафиксировать. На пенсии. Но и тогда, лучше потратить время на героин и симпатичных проституток, имхо. (С третьей стороны, мир совершенен, с наличием кокса найдутся юные сапиосексуалки которые тебе дадут забесплатно и в 80, если правильно посверкать золочённой оправой и тряхнуть седой и мудрой гривой. С четвёртой, у меня гривы не будет, разве что их к тому времени научатся отращивать, уж не знаю чем трясти мне. В любом случае, штанга только улучшит ситуацию) • ayoshi
• Спасибо большое за этот пост и картинку. Ровно таким образом мне много лет представляется картина распространения человеческого знания. Отдельно меня развлекает то, что две разведанные ветки могут лежать очень близко в "общем" пространстве, но в разведанном ("пропитанном") пространстве между ними очень далеко. А потом они делают ещё несколько шагов и вдруг соединяются. • 9000