Так, #извините, что не про сиськи, но тут, используя цифры от 1 до 9 по разу каждая, записали число e с точностью до ДЕСЯТКА СЕПТИЛЛИОНОВ десятичных знаков:
Не хотел бы я быть первооткрывателем подобного соотношения, потому что потом было б не избавиться от ощущения, что в этой вот хрени и состоял смысл жизни.
(т.к. 3^2=9, 2^2=4 и (6*7)*2+1=85, то произведение двух кучек цифр равно единице, и наблюдается второй замечательный предел (https://ru.wikipedia.org/wiki/%D0%97%D0%B0%D0%BC%D0%B5%D1%87%D0%B0%D1%82%D0%B5%D0%BB%D1%8C%D0%BD%D1%8B%D0%B5_%D0%BF%D1%80%D0%B5%D0%B4%D0%B5%D0%BB%D1%8B#.D0.92.D1.82.D0.BE.D1.80.D0.BE.D0.B9_.D0.B7.D0.B0.D0.BC.D0.B5.D1.87.D0.B0.D1.82.D0.B5.D0.BB.D1.8C.D0.BD.D1.8B.D0.B9_.D0.BF.D1.80.D0.B5.D0.B4.D0.B5.D0.BB ) с очень так неплохо устремившимся к бесконечности аргументом)
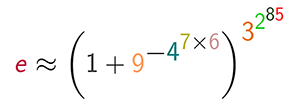
• НО КАК? В смысле, каким образом можно было такое открыть? • yole
• @yole: я вообще удивлен, что это произошло только сейчас. Ведь это реально не требует ничего кроме листочка бумаги (помимо проверки) • squadette
• ^^ самое сложным и неочевидным этапом было "сформулировать задачу", думаю. По образу и подобию других головоломок "используя девять цифр по разу, получите N". После этого всё довольно тривиально: 1). посмотреть на второй замечательный предел (он же, собственно, одно из возможных _определений_ e как такового), 2). понять, что из цифр надо собрать максимально большое N и 1/N, 3). привычным движением начать использовать двойное возведение в степень, 4). обратить внимание на 3^2=9 и 2^2=4, 5). дрожащими от предвкушения руками попытаться собрать из оставшихся цифр числа, удовлетворящие соотношению 2x+1=y, 6). найти 2*(6*7)+1=85, 7). [опционально] бегать по потолку и бухать три дня. • aldragon
• ^ и, строго говоря, есть сильное подозрение, что элементы решения случайно придумались раньше, чем сама задача :) • aldragon